はじめに
最近実際の財務諸表分析記事が多かったので本日は少し理論よりのお話。
ニューヨークの株式市場は、リーマンショック以降右肩上がり、日本の株式市場もアベノミクス以降上昇基調が続いています。
長らく上昇しか経験していないことから投資家の皆さんのリスク管理も甘くなりがちではないでしょうか。
そういう私も最近は、ほとんどがAIやネットベンチャーを中心としたリスク資産への投資割合がかなり高くなっています。
自戒も込めて、急に来るショックに備えたリスク管理について今回は考えていきたいと思います。
銀行等のリスク管理に使われるVaR
VaRという言葉、恐らく「なんとなく言葉は聞いたことがある」という方や「何それ」という方が多いと思います。
横文字で難しそうな印象を受けますが、定義は非常にシンプルです。
Value at Riskの略で日本語では予想最大損失と訳されます。
これは、一定期間あるリスク資産を保有した際に受ける恐れのある最大損失のことを言います。
一定期間というところは一つのポイントです。
一生を仮定してしまうとどんな株式も上場廃止になってしまう可能性はあるでしょうから、最大損失=投資額となってしまいリスク管理に役立ちません。
例えば、トヨタ自動車の1年間のVaRを考えてみましょう。
現在株価は7,581円です。
過去1年間の安値は、6月19日につけた5,787円で、例えば向こう一年間の最悪のシナリオは、前の1年間の安値だと仮定します。
そうすると1株あたりのVaRは、7,581円 – 5,787円 = 1,794円と計算できます。
1000株買っていればこれの1000倍になりますから18万円ですね。
実際にこのポートフォリオが最悪の場合いくらになるか?を考えて、それが会社や個人にとって受け入れ可能かを判断することに使われます。
デリバティブ等の複雑な金融商品が増えてきて、ポートフォリオのリスクが一見すると見えにくくなってきたことから開発された言葉で、銀行等が日次でのVaRの推移を把握してリスク管理に役立てています。
例えば三菱東京UFJのリスク管理のディスクロージャ誌の中にVaRの記載があります。
https://www.mufg.jp/ir/disclosure/2017mufg/pdf/data_all.pdf#page=58
VaRは実際にどうやって計算するの?
さて、言葉の定義がわかったところで、どうやって計算するのかを見てみましょう。
先ほどのトヨタ自動車の例では、過去1年間の安値を利用しました。
ただ、これが予想最大の損失といえるか?というと疑問ですよね。
例えば、新たなリコールでも発生しようものなら株価は急落するでしょうし、次の金融危機が今後来るかもしれません。
ではそのような予測をどうやってすればいいでしょう。
正規分布を使った仮定
今回は統計的な難しい話をするつもりはあまりありませんが、扱いやすいためによく使われる正規分布を利用した考え方を紹介しましょう。
正規分布は、例えば人の身長の分布をよく表すといわれています。

こんな分布になります。
グラフは20歳男性の身長の分布ですが、まず平均値である171.7cmの方が一番多くなっていることがわかります。
そしてその平均を中心に左右対称です。
株価も上がるか下がるかは、半々だろうからこんな分布に従うのではないか?という仮定を置くわけですね。
一つだけここで分布を理解する言葉を覚えましょう。
標準偏差 分布のばらつき具合を表す指標
この標準偏差が高いとばらつきが大きいということになります。
例えば有名校のテスト結果と田舎の公立校のテスト結果で考えましょう。
有名校はみんな勉強ができるため例えばテストが60点以下のような人は少なく平均点80点くらいに多く分布するでしょう。
一方で田舎の公立校であれば優秀な人もいれば、不良で全く勉強をしない人もいます。
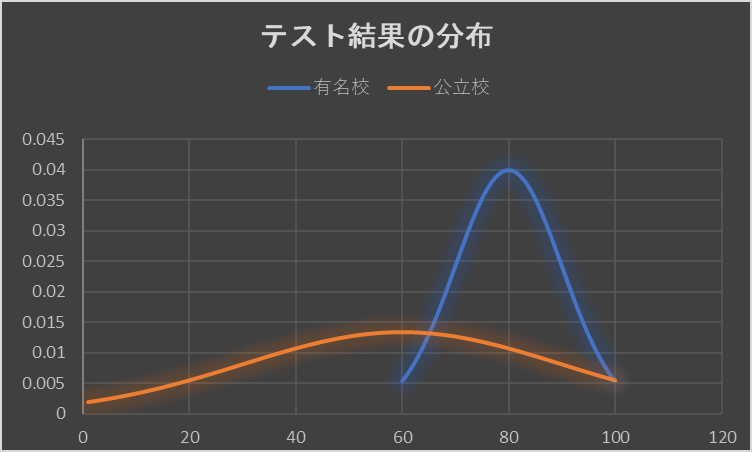
このようなグラフになるでしょうか。
有名校は、平均点80点付近に集中しているためばらつき(標準偏差)が小さい、公立校はいろいろな点数に分布があるため標準偏差が高いといいます。
これを株価に置きなおせば、ばらつきが高い=株価の変動が大きいということなので、リスクが高いということになります。
この標準偏差は、金融業界でリスクの指標としてよく利用されるので覚えておきましょう。ボラティリティと呼ばれます。なおテクニカル指標としてボリンジャーバンドを使っているかたはよく1σ、2σ等のパラメータを設定することになりますが、このσが標準偏差のことですね。
この正規分布と呼ばれる分布を使うと何がよいかというと、この平均と標準偏差がわかるだけで、株価がある一定以上、または以下になる確率がわかるということになります。
ほとんど起こりえない事象は取り除いて考える
さて、リスク管理の話に戻しましょう。
VaRは予想最大損失の把握のためではあるのですが、ほとんど起きえないことを考えても実はリスク管理に役立ちません。例えば、理論上は日本で大地震が起きた結果ほとんどの企業が倒産するという可能性はゼロではないでしょう。
ただ、その場合には、自分のポートフォリオのリスク管理・・・なんて言葉はいってられないでしょう。
そういうリスクを考えても意味がないのでその部分は切り離して考えます。
たとえばよくあるのは「確率が1%以下の事象は切り離して考えましょう。」といったことを行います。
これは、VaRが銀行のポートフォリオ管理といった実務の要請から生み出されたこともあり、現実的に役に立つようにある程度最大損失を予測するのに妥協をしてるんですね。
では1%以下の確率になる可能性というのはどこかというと、正規分布を仮定すると標準偏差の2.33倍平均からずれたところになります。
さっそくトヨタで計算してみましょう。
今回は1年分の株価で計算します。
2ステップで簡単にできます。
まず1年間の株価をダウンロードしましょう。
https://www.buffett-code.com/download
バフェット・コードから簡単にダウンロードできますし、Yahoo!Financeからでも入手できます。
Excelに落とすとSTDEVという関数を使って株価がある範囲を選択しましょう。
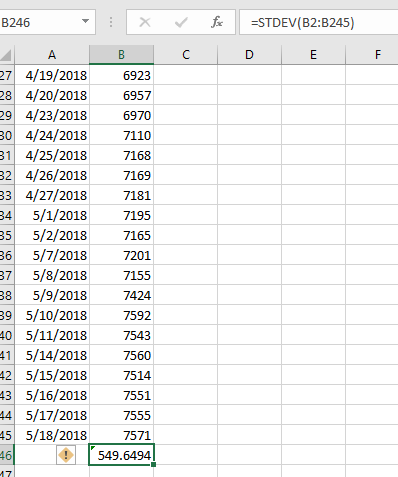
答えは549.6円となりました。
この標準偏差の2.33倍が1%以下で起こる下落幅です。1280円ですね。
VaRはこの1,280円×株式数で決まります。例えば100株持っていれば128万円の損ですね。
金融危機で通用しなかった正規分布を前提にしたVaR
今までみた損失管理は、今このブログで計算できるくらい簡単なのですごく便利です。
ただ、歴史を見るとブラックマンデーやリーマンショックのときにはこの予測したVaRよりもはるかに大きな損失が起きてしまい、皆さんもご存知の通り海外の証券会社が次々に倒産の危機にされされました。
ファイナンス理論全史という本によるとブラックマンデーのような株価下落が起きる確率は、宇宙ができてから現在にいたるまでに1度起きる確率よりも低いとのことです。
金融危機のときには不安が売り煽りにつながり、負のスパイラルになってしまうため身長の分布よりもはるかに異常値が出やすいということなんですね。
個人投資家が考えるべきVaRは?
金融危機の時に通用しないのであれば、不況時のリスク管理として利用するのはなかなか難しいです。
あくまで数字は参考程度に利用すべきでしょう。
では、個人投資家はどうすればいいのか。
もしあなたが優良企業に投資する堅実な投資家であるならば、恐らく過去の歴史を参考にするべきです。
特に直近であればリーマン・ショック時の数字が参考になるでしょう。
このブログでも何度も登場したコカ・コーラで見てみましょう。
外国株の株価はYahoo! Finance(US版)がExcelにダウンロードできて便利です。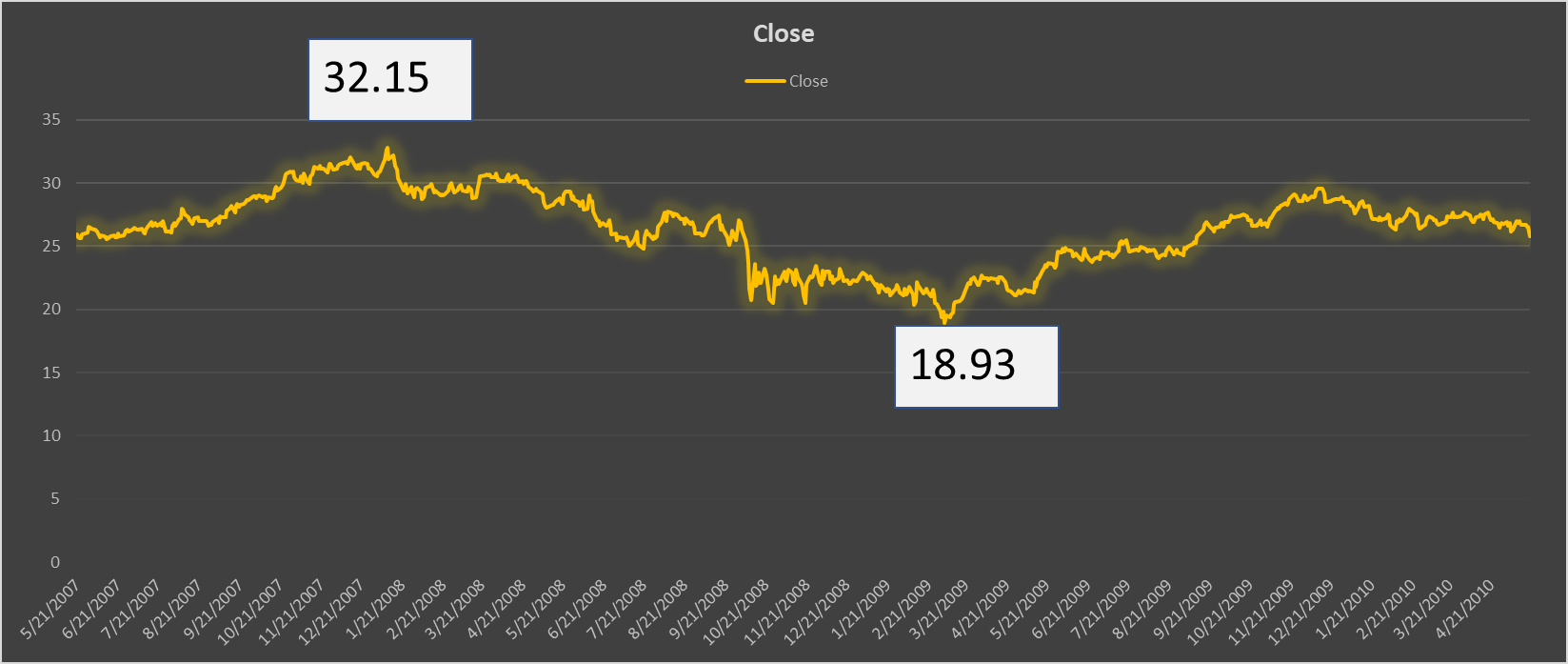
まず、高値32.15ドルから底値18.93ドルまで下落しています。下落幅は41.1%ですね。
長期でずっと放置するというスタイルの投資家であれば40%の損失に耐えなければならない恐れがあるということです。
実際には損切すればいいだろうということになると思います。
そこで、損切がうまくいく場合の最大損失として日次の下落幅を見てみましょう。
最も大きかった下落は2.05ドルでした。
下落幅は8.7%ですね。
損切がしっかりできる人はこれくらいを予想最大損失と考えてもいいでしょう。
世界的な優良企業であるコカ・コーラでもこれだけの損失を覚悟しないといけないのか、、と驚いたのは私だけではないかと思います。
終わりに
いかがだったでしょうか。
今回は、リスク管理の視点からVaRの解説をしてみました。
こんな面倒くさいことをしてられない!と感じられた方も多いかもしれません。
ただ、近年は、いきなり理由もなく株価が大幅下落といったことも少なくありません。
危機じゃないときにこそこのようなリスクを分析しておくことで、危機の際に焦らずに行動に移せるのではないかと思います。
好景気のときにこそこのようなシナリオ分析は意味があるのかもしれませんね。
今回の記事で登場したおすすめ書籍
日本長期信用銀行、UFJパートナーズ投信等で働いた経験のある田渕直也氏によるファイナンス理論の歴史解説書です。
難しいファイナンスを直感的にわかりやすく解説されています。
ここまで、多くの理論を簡単に解説した書籍はなかなかないような気がします。
もちろん、入門書なので、少し理論的に正確でない部分もありますが、まずファイナンスの雰囲気を知りたい方、どの分野に興味があるか発見したい方におススメです。

公認会計士。毎四半期、数百社くらいの決算資料を趣味で読みながら特徴的な決算について解説しています。「〇〇最終大幅赤字」といった表面的な報道があまり好きではなく、しっかり中身を語りたい。業界別に企業を比較しながら優良企業の強みにせまります。海外業務中心なので米国企業も強め。











コメントを残す